We all know the easy way to solve the quadratic equation, ax²+bx+c =0. We use the quadratic formula for roots.
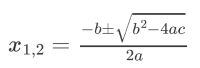
We also have access to similar formulae for roots of cubic equations and quartic equations.
The formula for roots of a cubic equation ax3+bx2+cx+d=0 is
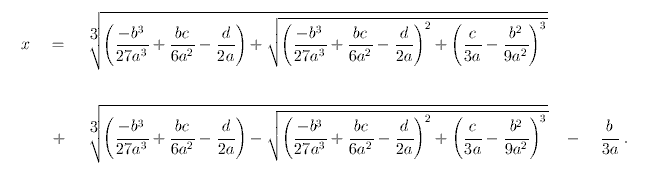
A similar complex looking formulae exist for roots of a quartic equation.
But mysteriously we do not have any such formula for roots of 5 or higher degree polynomials. It seems as if, we can not construct the solutions of a degree 5 or higher degree polynomials just by using addition, subtraction, multiplication, division, and radicals in its coefficients.
Why so? what is so special in this 5-degree polynomial? These were questions that haunted the young Frenchman Evariste Galois in the 18th century. He developed a new mathematical object called a “group” that solved this issue in a surprisingly cool way.
Permuting roots and symmetry
The answer lies in the symmetry of the roots.
The symmetry of the roots you may ask, what does that have to do with anything? What does it even mean?
Let’s plot the roots of two equations and see if we can make sense of it:
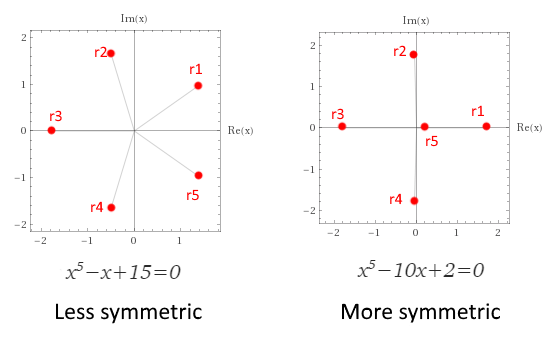
The left one is said to be less symmetric than the right one. This might surprise you because the word, symmetric is usually used if one can rotate or reflect the object without changing the way it looks. In that sense, the left picture looks more symmetric.
Let us see it with a few examples:
The star is more symmetric than the heart because aside from reflecting it, one can also rotate it.

But in our case, we are going to take a more general view of symmetries. We are not restricting ourselves to only reflections and rotations, any function that transforms the object without changing the way it looks is fair game. In the case of the roots, that means that any function that interchanges (permutes) the roots in any way is valid. More functions means more symmetric.
It turns out that in the right case, there are functions for permuting all the roots in any conceivable order, as many as 5!=120, so it is highly symmetric. But in the left case, if we interchange r₂↔r₄ using the transformation i↔−i we necessarily also interchange r₁↔r₅. This restricts us, and thus all conceivable permutations are not possible. It is less symmetric.
The functions that permute the roots are called “Automorphisms”, and if we group those automorphisms together we get what is called a “Group” (I will get back to better definitions of automorphisms and groups later on).
This means that the group that represents the symmetries of the roots is larger and more complex in the right case. In fact, the group in the right case is so complex that the roots cannot be described using radicals.
How do we know how complex a group is? To understand this we need a bit more theory.
The size of the quintic
First, let’s take a look at the size of a group. How do I know that there are some quintics that have a 5! large group?
A general quintic normally looks like this:
x⁵+ax⁴+bx³+cx²+dx+e=0
But if we take a more “root-centric” approach we can say that it looks like this:
(x−r₁)(x−r₂)(x−r₃)(x−r₄)(x−r₅)=
x⁵−(r₁+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…− r₁r₂r₃r₄r₅=0
That is, the constant a,b,c,d,e in the first equation is replaced by a symmetric combination of the roots:
r₁+r₂+r₃+r₄+r₅=a
r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c and d omitted for brevity)
r₁r₂r₃r₄r₅ = e
Looking at all the terms in detail, one discovers that interchanging the roots does not affect the equation (try it for b above for example). This is true for polynomials of any degree. Since we are able to interchange all the roots, we can draw the conclusion that the symmetry group for this general quintic is in fact all permutations, also called S₅ (the symmetric group of order 5).
Automorphism and the Fields
Now we are going to expand our definition of automorphisms a bit, as they are more than just functions that permute roots. In the process, we need to introduce something called “fields”. Why would we want to do that, you say? The reason is, that while working with roots and their permutations are fun, it’s a bit easier to work with fields and their automorphisms. It is exactly the same functions, don’t worry, just another way to look at them.
So, if the equation is, say x²–2=0, instead of working with the roots, r₁=√2, r₂=−√2 we are going to introduce the field Q(√2). This is all the rational numbers Q with an added √2. √2 is called a “field extension”. It looks like this: a+b√2 a,b∈ Q. To be able to describe the root of the equation we need the field Q(√2). For every field extension (and also other mathematical objects) we have a bunch of functions, σₙ, that sends a number to another unique number in the same field and follow the condition σ(a+b)=σ(a)+σ(b) and σ(ab)=σ(a)σ(b). σ is a function of the extension and does not touch the underlying field Q. These functions are called automorphisms. Incidentally, they also permute the roots. This is because for the root r:
r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (since σ does not touch Q (where a, b, c, d,e lives))
This means that σ(r) is also a solution to the equation. And since:
σ(r₁)−σ(r₂)=σ(r₁)+σ(−1)σ(r₂)=σ(r₁−r₂)≠0
the roots are distinct, so we have 5 of them, which must be the original 5. Thus σ must permute the roots.
Of course, this works for an equation of any degree.
Hence:
- We have our equation.
- That equation has a field that might contain an extension of a few radicals
- That field extension has a group, which is a collection of all its automorphisms.

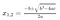


Comments
Post a Comment